<返回 径向直方图 有时也称为 : 角度直方图, 圆环直方图, 极坐标直方图

径向直方图

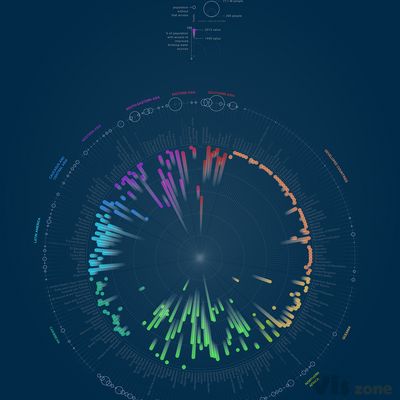
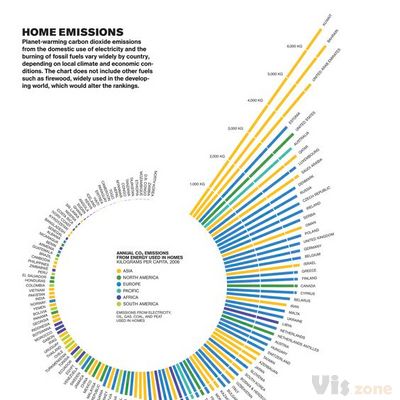
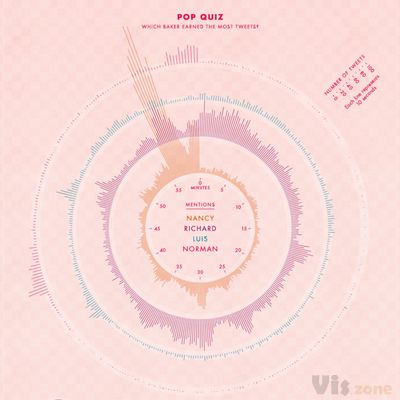
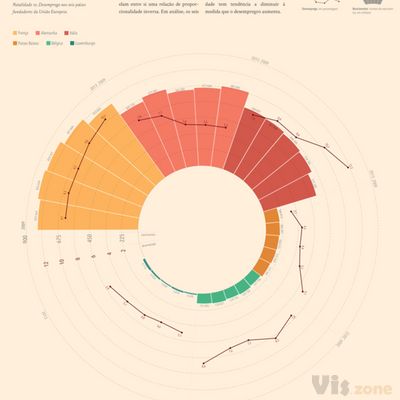
径向直方图有也称为「圆形直方图」或「极点直方图」，和其它径向图形类型，使用 极坐标系，而非笛卡尔坐标系。

极坐标系

极坐标系（polar coordinates）:

是指在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点O，称为极点。从O出发引一条射线Ox，称为极轴。再取定一个单位长度，通常规定角度取逆时针方向为正。
这样，平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定：
有序数对（ρ，θ）就称为P点的极坐标，记为P（ρ，θ）；ρ称为P点的极径，θ称为P点的极角。

极坐标系相关图形 ： 径向条形图 | 极地面积图 | 径向直方图 | 径向折线图 | 径向面积图 | 径向会聚 | 极线图

和直方图相比

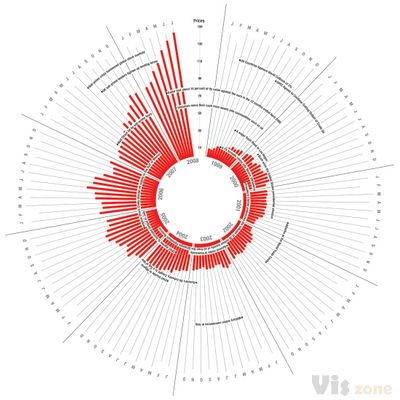
和普通的直方图相比，径向直方图能利用更多的空间，显示更多的数据，但不适合于阅读比较数值。
径向直方图使用同心圆网格来绘制条形图，每个圆圈表示一个数值刻度，而径向分隔线（从中心延伸出来的线）则用作区分不同类别或间隔。
刻度上较低的数值通常由中心点开始，然后数值会随着每个圆形往外增加，但也可以把任何外圆设为零值，这样里面的内圆就可用来显示负值。