<返回 双曲树 有时也称为 : 超树

双曲树

双曲树（英语：Hyperbolic Tree）是一种信息可视化和图形绘制方法，其灵感来自 双曲几何。

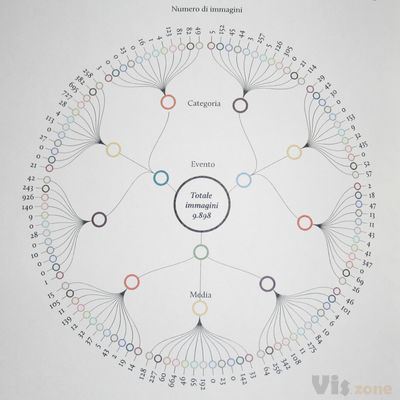
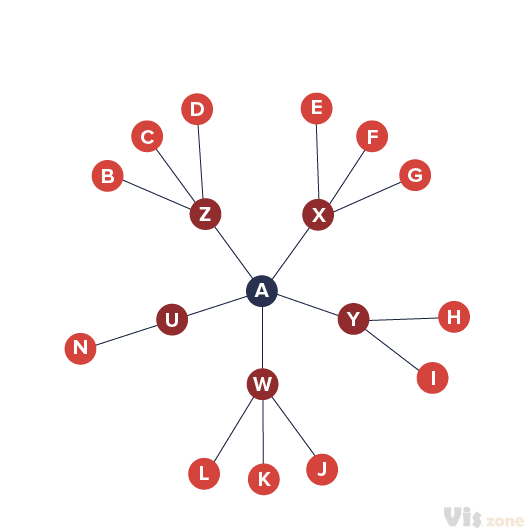
一个基本的双曲树。聚焦的节点被放置在中心，并给予更多的空间，而非聚焦的节点则被压缩在边界附近。

聚焦其他的节点会把它和它的子节点带到圆盘的中心，而树上不关注的部分则被压缩。

将分层数据显示为一棵树，由于每层的节点数量会呈指数级增长，因此会出现视觉上的混乱。对于一棵简单的二叉树来说，第 n 层的最大节点数是 2n，而分支较多的树的节点数增长得更快。因此，把树画成一个节点-链接图需要指数级的空间来显示。

双曲树采用双曲空间，其本质上比欧氏空间的“空间更大”。例如，在欧几里得空间中线性增加一个圆的半径，其周长会线性增加，而在双曲空间中同样的圆，其周长会呈指数级增加。利用这一特性，可以在双曲空间中以整洁的方式给树布局：把一个节点放在离其父节点足够远的地方，可以让该节点几乎拥有与其父节点相同的空间来布局自己的子节点。

通常利用双曲几何的庞加莱圆盘模型来展示双曲树，尽管也可以使用凯莱-克莱因模型。两者都是在一个单位圆盘中显示整个双曲平面，使整个树一次性可见。单位圆盘提供了一个平面的鱼眼透镜视图，更加强调焦点内的节点，而在靠近圆盘边界处可以显示更加远离焦点的节点。遍历双曲树需要对空间进行莫比乌斯变换，使新的节点成为焦点，并将层次结构的更高层次移出视野。

双曲几何

双曲几何又名罗氏几何（罗巴切夫斯基几何），是非欧几里德几何的一种特例。
与欧几里德几何的差别在于第五条公理（公设）－平行公设。在欧几里德几何中，若平面上有一条直线R和线外的一点P，则存在唯一的一条线满足通过P点且不与R相交（即R的平行线）。但在双曲几何中，至少可以找到两条相异的直线，且都通过P点，并不与R相交，因此它违反了平行公设。
然而，取代欧几里德几何中的平行公设的双曲几何本身并无矛盾之处，仍可以推得一系列属于它的定理，这也说明了平行公设独立于前四条公设，换句话说，无法由前四条公设推得平行公设。

层次结构数据

对有 层次关系的数据 进行可视化时，需要同时考虑如何将这种层级结构和指标同时进行展示。
既要让用户看明白数据的 层次结构，同时也要让用户看明白 指标间的“对比”

层次结构系列 ：多层饼图 | 多层环图 | 日出图 | 组织结构图 | 嵌套圆图 | 树状图 | 双曲树图 | 系统树图 | 凸树图 | 扇形图