<返回 欧拉图

欧拉图

1736年瑞士数学家欧拉（Euler）发表了图论的第一篇论文“哥尼斯堡七桥问题”。在当时的哥尼斯堡城有一条横贯全市的普雷格尔河，河中的两个岛与两岸用七座桥连结起来。当时那里的居民热衷于一个难题：有游人怎样不重复地走遍七桥，最后回到出发点。

哥尼斯堡七桥问题

为了解决这个问题，欧拉用 A,B,C,D 4个字母代替陆地，作为 4 个顶点，将联结两块陆地的桥用相应的线段表示，于是哥尼斯堡七桥问题就变成了图中，是否存在经过每条边一次且仅一次，经过所有的顶点的回路问题了。欧拉在论文中指出，这样的回路是不存在的。
图的环游(tour)是指经过图的每条边至少一次的闭途位。欧拉环游是经过每条边恰好一次的环游。一个图若包含欧拉环游/或欧拉回路，则称为欧拉图(Euleriangraph)。

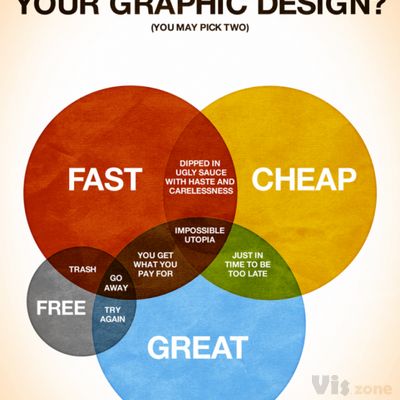
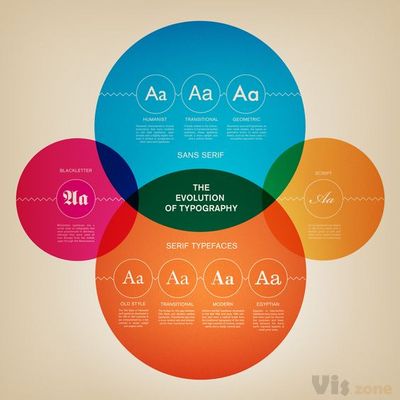
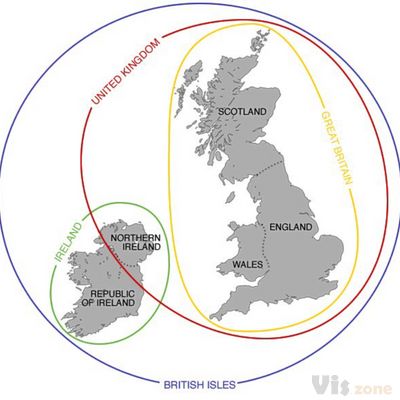
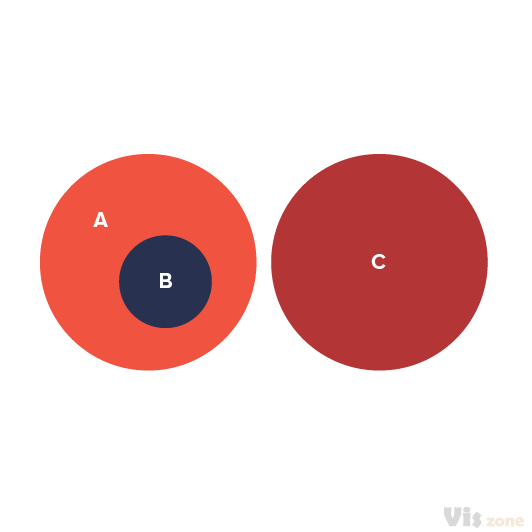
在欧拉图中，曲线的大小或形状并不重要：图表的意义在于它们如何重叠。由每条曲线限定的区域之间的空间关系(重叠、包容或两者都不)对应于集合论关系(相交、子集和不相交)。

欧拉图的数学定义

1. 通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路。
2. 通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路。
3. 具有欧拉回路的无向图或有向图称为欧拉图。
4. 具有欧拉通路但不具有欧拉回路的无向图或有向图称为半欧拉图。
5. 有向图也可以有类似的定义。

非形式化地讲，欧拉图就是从任意一个点开始都可以一笔画完整个图，半欧拉图必须从某个点开始才能一笔画完整个图。